I numeri primi
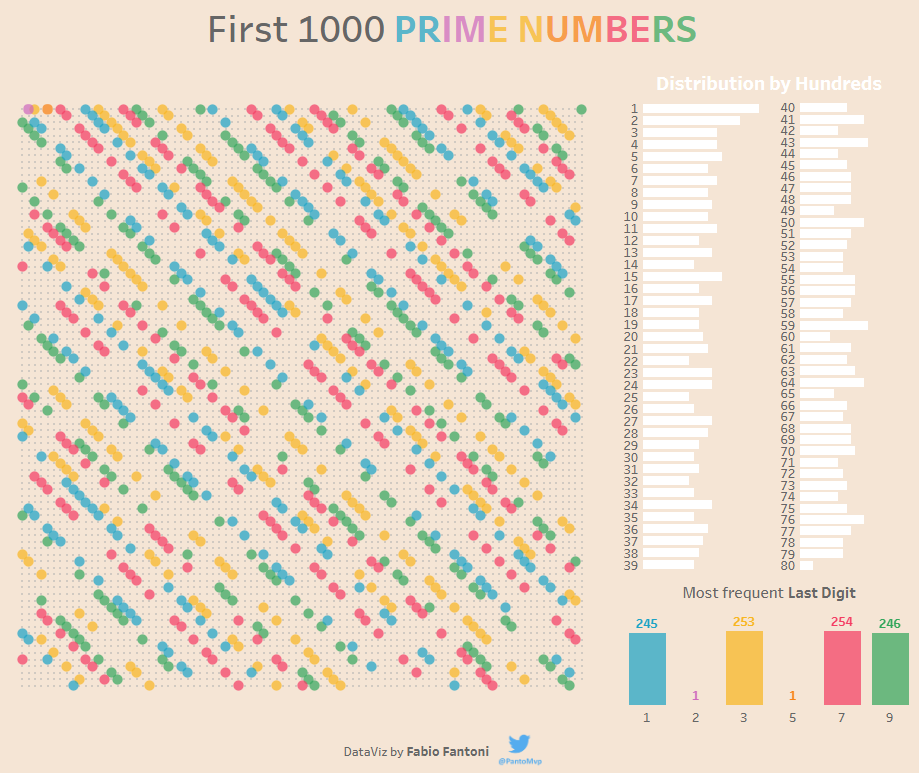
Cliccando sulla immagine seguente, ti si aprirà una pagina contenente un grafico interattivo, che mostra i primi 1000 numeri primi. Osservalo con attenzione e prova a rispondere, sul quaderno, alle domande seguenti.
- Il numero 6833 è un numero primo?
Come è rappresentato nel grafico? - Il numero 7387 è un numero primo?
Come è rappresentato nel grafico? - Quanti numeri primi ci sono minori di 100?
- Quanti numeri primi ci sono compresi tra 100 e 200 (cioè contemporaneamente più grandi di 100 ma più piccoli di 200)?
- Quanti numeri primi ci sono compresi tra 200 e 300?
- Quanti numeri primi ci sono minori di 1000?
Per rispondere, devi fare un calcolo: scrivi sul quaderno sia il calcolo che fai, sia il risultato. - Quanti numeri primi ci sono compresi tra 1000 e 2000 (cioè contemporaneamente più grandi di 1000 ma più piccoli di 2000)?
Per rispondere, devi fare un calcolo: scrivi sul quaderno sia il calcolo che fai, sia il risultato. - Quanti numeri primi ci sono compresi tra 2000 e 3000 (cioè contemporaneamente più grandi di 1000 ma più piccoli di 2000)?
Per rispondere, devi fare un calcolo: scrivi sul quaderno sia il calcolo che fai, sia il risultato. - Dei primi 1000 numeri primi, quanti finiscono con la cifra 0?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 1?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 2?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 3?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 4?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 5?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 6?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 7?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 8?
- Dei primi 1000 numeri primi, quanti finiscono con la cifra 9?
- Secondo te, perché ho aggiunto questa domanda?