Omotetie
Ricorda:
- una omotetia di centro O è una trasformazione che manda ogni punto P del piano in un punto P’ che si trova sulla retta OP;
- se il rapporto dell’omotetia è positivo (+), il punto P’ si trova dalla stessa parte di P rispetto ad O;
- se il rapporto dell’omotetia è negativo (-), il punto P’ si trova dalla parte opposta di P rispetto ad O;
- il rapporto tra la lunghezza del segmento OP’ e la lunghezza del segmento OP è pari al valore assoluto del rapporto dell’omotetia (in altre parole: se il rapporto dell’omotetia è +4 o -4, la distanza di P’ da O è il quadruplo della distanza di P da O; se il rapporto dell’omotetia è -1/2 o +1/2, la distanza di P’ da O è la metà della distanza di P da O).
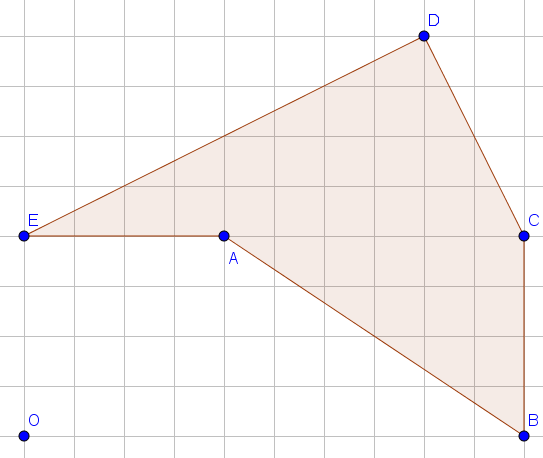
Esercizio 1
Ricopia sul quaderno la figura, contando bene i quadretti (ad ogni quadretto sulla figura, fai corrispondere un quadretto sul quaderno).
Disegna il poligono A’B’C’D’E’, immagine di ABCDE in una omotetia di centro O e rapporto +1/4.
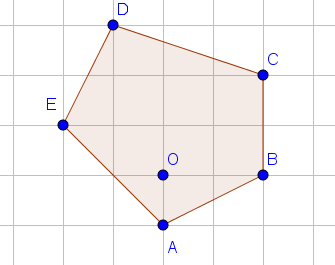
Esercizio 2
Ricopia sul quaderno la figura, contando bene i quadretti (ad ogni quadretto sulla figura, fai corrispondere un quadretto sul quaderno).
Disegna il poligono A’B’C’D’E’, immagine di ABCDE in una omotetia di centro O e rapporto +3.
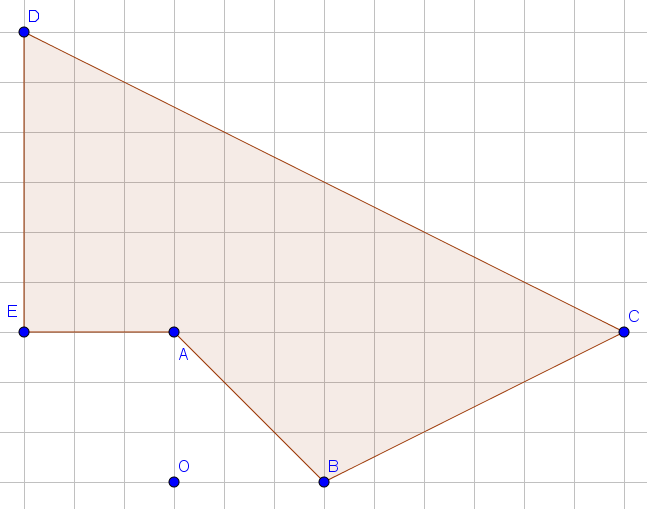
Esercizio 3
Ricopia sul quaderno la figura, contando bene i quadretti (ad ogni quadretto sulla figura, fai corrispondere un quadretto sul quaderno).
Disegna il poligono A’B’C’D’E’, immagine di ABCDE in una omotetia di centro O e rapporto -1/3.
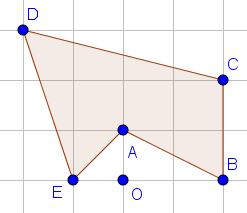
Esercizio 4
Ricopia sul quaderno la figura, contando bene i quadretti (ad ogni quadretto sulla figura, fai corrispondere un quadretto sul quaderno).
Disegna il poligono A’B’C’D’E’, immagine di ABCDE in una omotetia di centro O e rapporto -2.