Nell’ultima lezione di aritmetica abbiamo imparato come costruire segmenti aventi per lunghezza la radice quadrata di 2, di 3 e di tutti i numeri naturali.
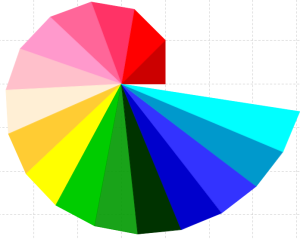
Questi segmenti possono venir riportati sulla retta numerica (come abbiamo fatto in classe) o costruiti “uno attorno all’altro”, a formare una spirale: si parte da un triagolo rettangolo isoscele e si procede come ho accenntato in classe, disegnando così una figura che prende il nome di spirale di Teodoro.
Se la spiegazione in classe non è stata abbastanza chiara, o se vuoi approfondire l’argomento, ecco alcuni link che puoi consultare:
In questi link, non vengono date istruzioni precise a proposito di quali strumenti di GeoGebra utilizzare, ma solo riguardanti la costruzione geometrica: se sei in difficoltà, mandami un messaggio di posta elettronica, e ti invierò un videotutorial con le istruzioni precise.
Per il 22 maggio 2017 mi aspetto di ricevere (per posta elettronica o su una chiavetta usb) un tuo file, dove la spirale sia costruita almeno fino al segmento di lunghezza radicequadrata di 17.
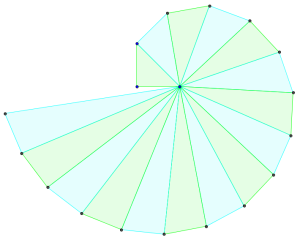
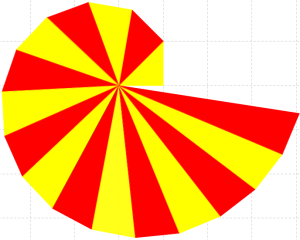
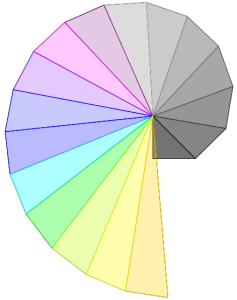
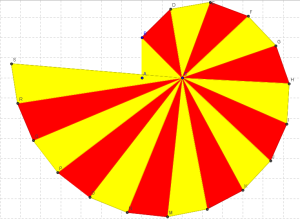
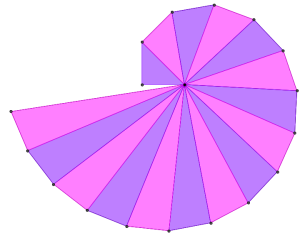
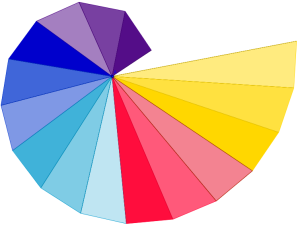
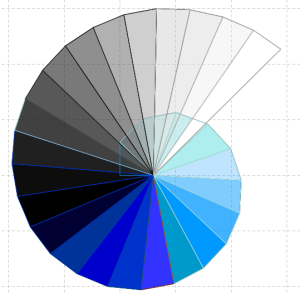
Ecco alcuni dei disegni dei miei alunni di qualche anni fa:
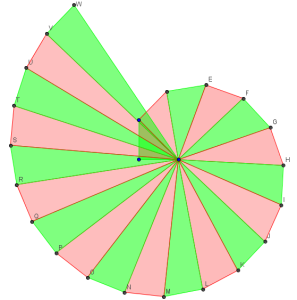
La seguente immagine non è di un alunno, ma di una collega: grazie a Daniela Molinari, che i miei studenti conoscono già per le sue recensioni su amolamatematica.it.
Daniela ha lasciato tutti gli elementi della costruzione e ha colorato nello stesso modo tutti i triangoli. A mio parere l’effetto è quello di lasciare che siano evidenti (dalla costruzione, appunto) le proprietà della figura e di dare un’immagine complessiva della spirale, piuttosto che dei suoi singoli spicchi.