Quarto allenamento in vista dei Campionati

Ecco il quarto allenamento on-line di questo anno per tutti gli alunni della scuola “Piero Calamandrei” di Chirignago che desiderano allenarsi per la semifinale dei Campionati Internazionali di Giochi Matematici. Aspetto le vostre risposte: potete consegnarmele a scuola, su un foglietto, o inviarmele per posta elettronica all’indirizzo

sofia.sabatti@comprensivocolombo.it

(se le scriveste tra i commenti qui sotto, rischiereste di “spoilerare”, e non sarebbe bello…)! Non dimenticatevi di indicarmi anche il vostro nome e il vostro cognome.

La corsa delle bandierine

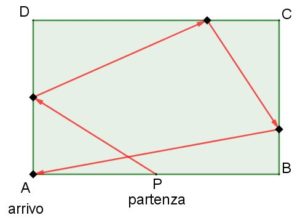
La corsa delle bandierine si svolge in un campo rettangolare di 80 m per 50 m.

Ogni concorrente corre da solo, partendo dal punto medio del lato AB con quattro bandierine in mano. Il suo obiettivo è piantare una bandierina su ciascuno dei lati AD, DC e CB, in questo ordine, e l’ultima bandierina sul vertice A.

Dove dovrebbe attaccare le bandierine un concorrente per rendere il proprio percorso più breve possibile?

(liberamente tratto da Eduardo Veloso e Josè Paulo Viana, Desafios 4. Problemas e histórias da matemática no público, edições Afrontamento, 1995)

Risposte al terzo allenamento in vista dei Campionati

Ho ricevuto quattro risposte corrette al problema “Send more money“, questa volta da tre ragazze e un ragazzo, tutti di prima e seconda media.

Le lettere del messaggio cifrato corrispondono ai numeri in questo modo:
S=9
E=5
N=6
D=7
M=1
O=0
R=8
Y=2
Quindi, per accontentare harry, Elisabeth dovrà madargli 10 652 dollari canadesi; l’auto usata che Harry vuole comprarsi costa 9 567 dollari canadesi e il treno di gomme invernali costa 1085.

Solo una ragazza mi ha spiegato per benino come ha fatto a trovare la risposta e il suo lavoro mette in evidenza alcuni tentativi, ma anche tanto ragionamento.

Ad esempio: la lettera M non può che corrispondere al numero 1 perchè la somma di due numeri (ad una cifra) non può essere maggiore o uguale a 20 (ossia deve essere minore o uguale a 19 e quindi, se è un numero di due cifre, la cifra delle decine è sicuramente 1): questo implica che quando faccio S+M (ed eventualmente ci aggiungo un riporto che al massimo è 1), essendo S e M al massimo 8 e 9 comunque arrivo ad un numero che come cifra delle decine ha 1.

Ma adesso, S+1 (più un eventuale riporto al massimo di 1) deve dare un numero che come cifra delle decine ha 1 e come cifra delle unità ha O.
Se S fosse 9 e ci fosse il riporto di 1, verrebbe O=1 il che non può essere perchè già M è 1.
Se S fosse 9, e non ci fosse riporto, verrebbe O=0.
Se S fosse 8 e ci fosse il riporto di 1, verrebbe O=0.
Se S fosse 8 e non ci fosse il riporto, non funziona perché la somma sarebbe di una cifra sola.
Quindi siamo certi che O=0.

I ragionamenti di Ambra non si fermano qui, ma… forse è meglio se ciascuno di voi prova ad andare avanti da solo, non pensate?

Che cosa abbiamo imparato?

Giada, Gioia, Ambra e Christian, che sono riusciti a risolvere questo problema, forse non sono riusciti ad imparare niente di nuovo. Chi ci ha provato e non ce l’ha fatta, potrebbe trarre ispirazione dalla seguente riflessione (parto da 6, perché 5 cose le abbiamo già imparate commentando i primi due allenamenti).

6. Tentativi e ragionamenti devono andare a braccetto

Molto spesso siamo convinti che per risolvere un problema di matematica si debba cercare l’operazione da fare, farla e dare la risposta.
Spesso non è così: spesso bisogna provare, fare dei tentativi, verificare se funzionano.
Ora, nella maggior parte dei casi – fortunatamente – abbiamo la possibilità di accompagnare le nostre prove con dei ragionamenti, che ci consentono di limitare il numero di tentativi da fare. Ragionare e provare non sono due strade alternative, ma sono due modi di agire che possono l’uno accompagnare l’altro di continuo.

Come dire: non dobbiamo avere paura di fare dei tentativi, ma possiamo anche cercare di capire sempre se un tentativo che ci viene in mente può essere escluso a priori con qualche ragionamento.