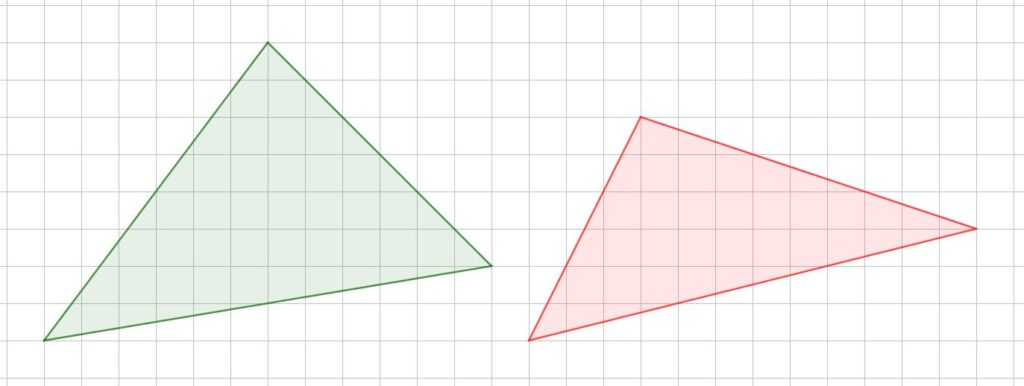
Altezze e ortocentro di un triangolo su carta a quadretti
Disegna sul tuo quaderno dei triangoli “uguali” a questi. Come in classe quando copi dalla lavagna, per “uguali” si intende qui che abbiano la stessa forma, anche se (ovviamente) le dimensioni saranno diverse. Un quadretto dei disegni qui sotto riportati deve essere considerato “uguale” a un quadretto del tuo quaderno.
Disegnato il triangolo, disegna le sue altezze e trova il suo ortocentro, usando (come strumenti da disegno) una matita ben appuntita, una riga (anche un pezzo di cartoncino rigido va bene) e la carta a quadretti.
Se non ricordi più come fare, puoi guardare il videotutorial incorporato più sotto. Attento, però: il triangolo disegnato nel videotutorial non ha i lati inclinati nello stesso modo di quelli del triangolo che ti è stato assegnato. Cerca quindi (guardando il videotutorial e ripassando la lezione svolta in classe lunedì 18 novembre) di capire qual è il procedimento da seguire e poi di applicarlo al triangolo che è qui disegnato.