Se non fai errori, stai lavorando su problemi che non sono abbastanza difficili. E questo è un grosso errore.
(Frank Wikzek)
Lunedì 27 febbraio 2018, in terza C [1], abbiamo raccolto le fila di un lungo lavoro fatto in classe nelle scorse settimane. Ogni alunno aveva costruito, a partire da sviluppi piani stampati da me su cartoncini, una dozzina di poliedri. In piccoli gruppi, in classe, avevano dovuto contare, per ciascuno dei loro poliedri, il numero dei suoi spigoli, dei suoi vertici e delle sue facce. Tutti questi numeri erano stati inseriti in una tabella che i ragazzi avevano dovuto analizzare per vedere se riuscivano a trovare qualche regolarità, in particolare se riuscivano a trovare una relazione valida per tutti i poliedri analizzati che legasse S (il numero degli spigoli), V (il numero dei vertici) e F (il numero delle facce).
Raccogliere le fila ha significato constatare che solo [2] una alunna (Anna) aveva scoperto qualcosa, accorgendosi che per ciascuno dei poliedri i cui dati avevamo inserito in tabella accadeva che V-S+F=2.
Dapprima, malfidati come abbiamo imparato ad essere, abbiamo verificato che in tutti i casi da noi studiati (una ventina in tutto) questa relazione fosse valida. Per farlo abbiamo semplicemente calcolato V-S+F per tutti i poliedri costruiti e schedati: abbiamo visto che il risultato veniva sempre 2.
Ovviamente ho fatto i complimenti ad Anna e ho detto a tutti che questa relazione è nota come “relazione di Eulero”; i ragazzi erano entusiasti, stupiti del fatto che valesse sempre, anche per i poliedri più strani che avevamo costruito, come ad esempio, un cubo a cui mancava un cubetto:
Ho però presto frenato i loro entusiasmi insinuando un dubbio: siamo certi che questa relazione sia valida per tutti i poliedri?
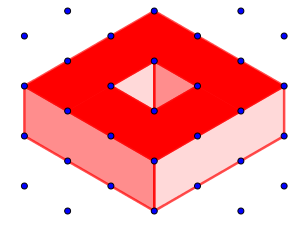
Poiché l’ora volgeva al termine, ho detto loro di provare a fare lo stesso calcolo per questo poliedro, che avevamo disegnato su carta isometrica in una delle precedenti lezioni [3]:
L’ho detto convinta che, essendo questo poliedro “buco”, la relazione di Eulero non valesse; e invece, proprio mentre suonava la campanella, noi stavamo contando i 16 vertici, i 24 spigoli e le 10 facce (1 sopra, 1 sotto, 4 esterne e 4 interne), accorgendoci che V-S+F=16-24+10 faceva comunque 2.
Me ne sono uscita dicendo che c’era qualcosa che non andava, ma non sapevo cosa: o avevamo sbagliato a contare, o io avevo preso un abbaglio!
Grazie al cielo, proprio quel pomeriggio, ho partecipato ad una lezione di aggionamento ed approfondimento sulla Geometria, tenuta dalla professoressa Maria Dedò a Padova, presso il Liceo artistico “Pietro Selvatico“. Il titolo della conferenza era proprio “V-S+F=2 ovvero… salviamo la geometria dall’estinzione!”
Non mi sono fatta sfuggire l’occasione e ho proprio chiesto alla professoressa Dedò che cosa ci fosse che non andava nel mio “controesempio”: non essendo omeomorfo ad una sfera, ma ad un toro, la costante di Eulero non sarebbe dovuta valere 0? E così mi sono accorta che il problema stava nella definizione di poliedro. Se le facce di un poliedro devono essere dei poligoni, e se i poligoni devono essere delle parti di piano delimitate da una linea spezzata chiusa, il solido che avevo preso di esempio non era esattamente un poliedro (la faccia di sopra e la faccia di sotto non sono dei poligoni… sono parti di piano delimitate da due spezzate, una dentro l’altra).
Il giorno dopo, tornata a scuola, ho raccontato ai ragazzi della lezione di lunedì pomeriggio, e ho portato loro, trionfante, un solido (questa volta un vero poliedro) che avevamo costruito con il Polydron durante la lezione del pomeriggio prima:
Due ragazzi (Luca e Thomas) in breve tempo hanno contato 60 vertici, 135 spigoli e 75 facce: quindi V-S+F=60-135+75 davvero non veniva 2, ma 0.
A questo punto ho chiesto ai ragazzi, divisi in gruppetti da 3 o 4 persone ciascuno, di costruire altri poliedri di questo tipo, con un buco in mezzo, per vedere se il valore di V-S+F continuasse ad essere 0.
Questo è il poliedro costruito da Nensi, Desiré, Sara e Vanessa:
Questo il poliedro costruito da Silvia, Shanty, Marco e Daniel:
Questo il poliedro costruito da Anna, Luca, Ambra e Sara:
Dei vari gruppi, quello che ha avuto più difficoltà a contare vertici, spigoli e facce è stato il gruppo che ha costruito l’ultimo dei solidi qui sopra, perché in esso c’era sì una struttura che si ripeteva 9 volte, ma questa struttura non era tra “i solidi noti”.
Udaya, Marco e Riccardo hanno costruito questo solido:
In questo gruppo gli alunni hanno usato più tessere di Polydron per una stessa faccia: in alto si vedono quindi tante tessere diverse, ma le facce sono “solo” quattro trapezi (ciascuno formato da tre tessere triangolari: una rossa, una verde e una gialla) e quattro triangoli (le tessere blu); così pure, esternamente, ci sono quattro facce formate da quattro tessere quadrate ciascuna e quattro facce formate da due tessere quadrate ciascuna.
E adesso veniamo agli “errori”. Di un primo errore, il mio, ne abbiamo già parlato. E forse proprio questo mio primo errore ha male instradato due gruppi, che hanno costruito due solidi con due facce parallele che però non sono dei poligoni, ma delle superfici “con un buco”.
Questo il solido costruito da Andrea, Alessio, Matteo e Riccardo:
Questo il solido costruito da Luca, Ilenia e Sara:
Anche a questi due gruppi, però, la somma V-S+F veniva 0. E io non mi capacitavo…
Com’è che nel mio solido/non-poliedro (anche se buco) la somma V-S+F non veniva 0, mentre nei solidi/non-poliedri buchi dei miei alunni invece sì?
Mi sono messa ad ascoltare come facevano i conti e mi sono accorta che (in entrambi i casi) consideravano le due facce parallele come suddivise in tante facce più piccole (una per ogni tessera del Polydron usata) e così ogni giuntura tra due tessere diventava uno spigolo. La mia prima reazione è stata, più o meno, questa: “Ma così state sommando errore ad errore! Il primo errore è stato che avete costruito un solido con due facce “buche” che quindi non è un poliedro, il secondo errore è che avete contato facce ciò che facce non sono e spigoli ciò che spigoli non sono”.
Tornata a casa ci ho pensato su.
E ho pensato che, in realtà, il loro doppio errore apre la strada ad una riflessione profonda, che vedrò di proporre loro nella prossima lezione. La caratteristica di Eulero non appartiene solo ai poliedri. Appartiene ad un qualsiasi grafo [4] disegnato su una superficie: V indicherà il numero dei nodi del grafo, S indicherà il numero degli archi che connettono i nodi, F indicherà il numero delle regioni in cui la superficie risulta divisa. Se il grafo sarà disegnato su una superficie omeomorfa alla sfera, V-S+F sarà uguale a 2; se il grafo sarà disegnato su una superficie omeomorfa ad un toro, V-S+F sarà uguale a 0. Gli alunni di questo gruppo, di fatto, non hanno costruito un poliedro; ma hanno comunque evidenziato, sulla superficie del loro solido, un grafo per il quale comunque vale la relazione di Eulero: grandi, no?
[1] Si tratta della classe terza C della Scuola secondaria di primo grado “Piero Calamandrei” di Chirignago, Venezia.
[2] Forse non è il caso di dire “solo”, visto che il primo matematico ad accorgersi di questo fatto è stato Eulero, vissuto nel XVIII secolo.
[3] Su carta isometrica gli alunni avevano disegnato, durante le lezioni immediatamente precedenti a questa, vari solidi, copiandoli dal vero da solidi costruiti da me giustapponendo vari cubetti.
[4] In realtà non è che sia proprio un grafo qualsiasi. Deve essere un grafo che assomiglia ad un poliedro…! Ogni spigolo deve essere adiacente ad esattamente due facce e contenere esattamente due vertici, dati due vertici deve esistere al massimo uno spigolo che li contenga entrambi, date due facce, deve esistere al massimo uno spigolo adiacente ad entrambe, ogni vertice deve essere adiacente ad almeno tre facce e ogni faccia deve contenere almeno tre vertici.